Таблица баллов ЕГЭ 2021
Шкала перевода первичных баллов ЕГЭ по математике профиль в тестовое. Минимальный проходной балл - 27
Тест ЕГЭ от "Яндекс.Репетитор"
Пройдите тест ЕГЭ на портале "Яндекс.Репетитор" и определите уровень своей подготовки к ЕГЭ по профильной математике
10.09.2021 Задание 14 ЕГЭ 2021
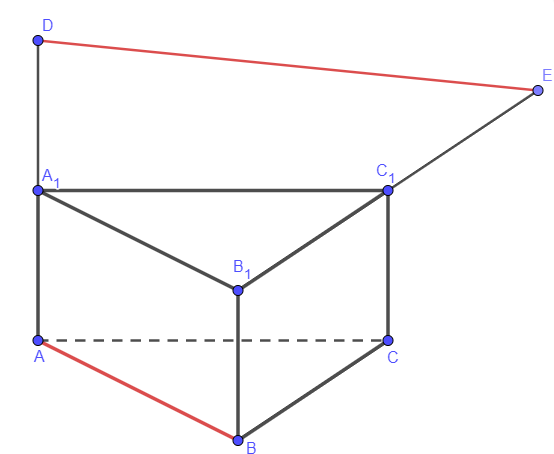
В оcновании правильной треугольной призмы ABCA1B1C1 лежит треугольник ABC. На прямой AA1 отмечена точка D так, что точка A1 – середина отрезка AD. На прямой B1C1 отмечена точка E так, что точка C1 – середина отрезка B1E.
а) Докажите, что прямые A1B1 и DE перпендикулярны.
б) Найдите расстояние между прямыми AB и DE, если AB=3, AA1=1.
11.07.2021 Справочные материалы ЕГЭ База ФИПИ
11.07.2021 Все формулы в одном документе
22.03.2021 Свойства логарифмов
Определение логарифма, логарифм суммы/разности, переход к новому основанию.
22.03.2021 Формулы сокращенного умножения
Формулы разности квадратов, квадрата суммы/разности, куба суммы/разности, разложение квадратного трехчлена на множители
22.03.2021 Свойства арифметических корней
Произведение/частное выражений с арифметическим корнем, возведение встепень