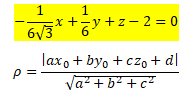Задание 14 ЕГЭ 2021

В оcновании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник ABC. На прямой AA₁ отмечена точка D так, что точка A₁ – середина отрезка AD. На прямой B₁C₁ отмечена точка E так, что точка C₁ – середина отрезка B₁E.

а) Докажите, что прямые A₁B₁ и DE перпендикулярны.

б) Найдите расстояние между прямыми AB и DE, если AB=3, AA₁=1.

а)

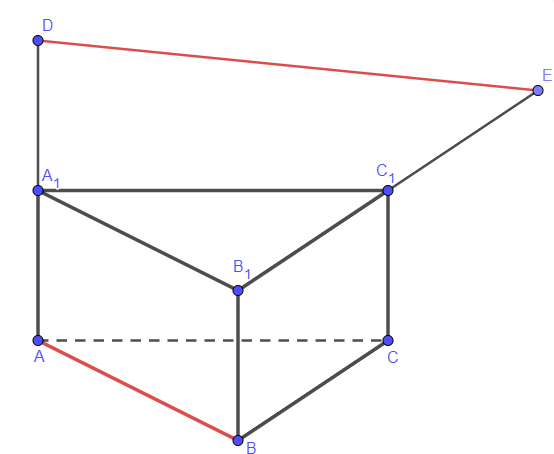
Для доказательства перпендикулярности прямых используем метод координат. Введем систему координат, как показано на чертеже:

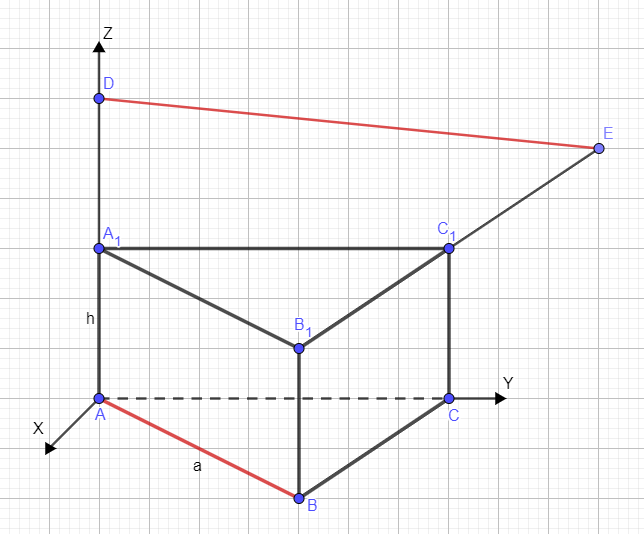
Доказательство перпендикулярности прямых координатным методом основано на том, что скалярное произведение двух перпендикулярных векторов равно нулю.

То есть, сначала найдем координаты векторов 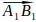 и 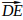, затем, вычислим их скалярное произведение. Если прямые перпендикулярны, то скалярное произведение будет равно нулю.

Пусть AA₁=h, AB=a. Найдем координаты Точек A₁, B₁, D, E.

Построим вспомогательный чертеж треугольника ABC (вид сверху):

Из чертежа следует, что:

• проекция стороны a на ось AX (a_x) равна высоте треугольника ABC;

• проекция стороны a на ось AY (a_y) равна половине стороны треугольника ABC.

Тогда:

Точка А₁ имеет координаты: А₁(0;0;h)

Точка В₁ имеет координаты: В₁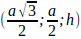

Вектор 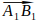 имеет координаты: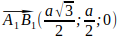 

Аналогично находим координаты вектора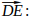 

D(0;0;2h)

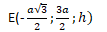
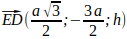
Скалярное произведение векторов:

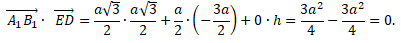
Значит, прямые A₁B₁ и DE перпендикулярны.

Ч.т.д.

б) Расстояние между прямыми AB и DE найдем так же, методом координат.

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой.
Допустим, будем находить расстояние от точки А до плоскости DEK, проведенной параллельно AB. Найдем координаты точки А, координаты плоскости DEK, затем, по формуле расстояния от точки до плоскости найдем расстояние между ними.

Для построения плоскости DEK проведем через точку E прямую a₁, параллельную AB и отметим на ней точку K так, что EK=AB

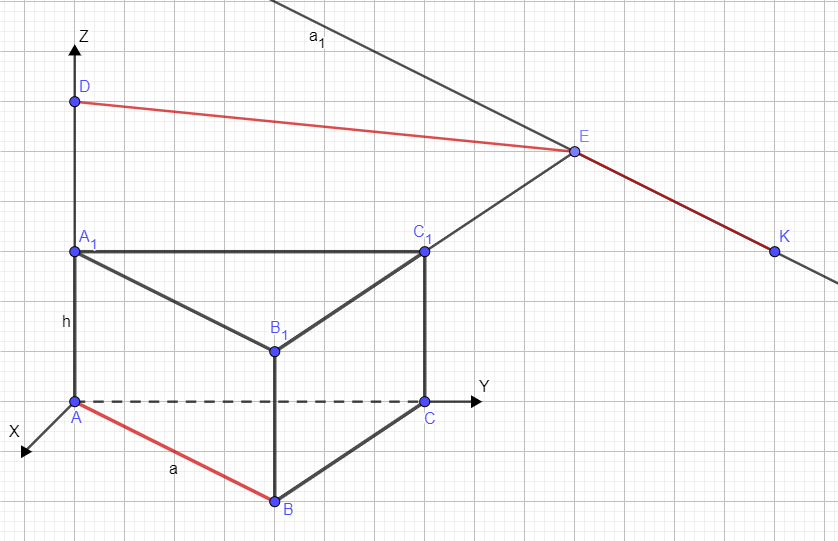
Отметим проекцию точки K на плоскость XY на нашем вспомогательном чертеже:

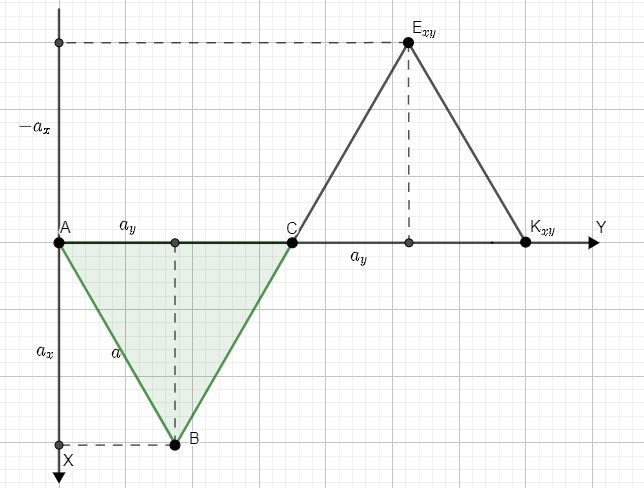
По условию a=3, h=1

Из чертежа следует:

A(0;0;0);

K(0;6;1);

D(0;0;2);

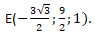
 Общее уравнение плоскости имеет вид: ax+by+cz+d=0 (1)

 Для нахождения уравнения плоскости DEK запишем систему уравнений (1) и подставим вместо x,y,z координаты точек K,D,E:

 

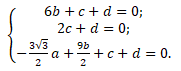
Решая систему, находим:

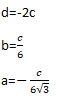
Подставив коэффициенты a,b,c,d в уравнение (1) получим искомое уравнение плоскости:

.  Поделим обе части на с: